Regression is a technique used to predict future values based on known values. For instance, linear regression allows us to predict what an unknown Y value will be, given a series of known X and Y’s, and a given X value.
Given the following, it’s easy to see the pattern. But assuming no obvious pattern exists, regression can help us determine what the Y value will be given our known X values.
| X | Y |
| 2 | 3 |
| 4 | 6 |
| 6 | 9 |
| 8 | 12 |
| 10 | 15 |
| 12 | |
| 14 |
The X value is known as the independent variable, the “predictor variable”, while the Y value is the value you’re being predicted.
The linear regression (or “least squares regression”) equation is Y’ = a + bX
- Y’ (Y-prime) is the predicted Y value for the X value
- a is the estimated value of Y when X is 0
- b is the slope (the average change in Y’ for each change in X)
- X is any value of the independent variable
There are additional formulas for both a and b.
Let’s take a look at the following data-set, that compares the number of calls made for a product against the number of sales:
| Calls (X) | Sales (Y) |
| 20 | 30 |
| 40 | 60 |
| 20 | 40 |
| 30 | 60 |
| 10 | 30 |
| 10 | 40 |
| 20 | 40 |
| 20 | 50 |
| 20 | 30 |
| 30 | 70 |
| 220 | 450 |
First we need to calculate the sum of X-squared, Y-squared and X*Y:
| Calls (X) | Sales (Y) | X2 | Y2 | XY | |
| 20 | 30 | 400 | 900 | 600 | |
| 40 | 60 | 1600 | 3600 | 2400 | |
| 20 | 40 | 400 | 1600 | 800 | |
| 30 | 60 | 900 | 3600 | 1800 | |
| 10 | 30 | 100 | 900 | 300 | |
| 10 | 40 | 100 | 1600 | 400 | |
| 20 | 40 | 400 | 1600 | 800 | |
| 20 | 50 | 400 | 2500 | 1000 | |
| 20 | 30 | 400 | 900 | 600 | |
| 30 | 70 | 900 | 4900 | 2100 | |
| Total | 220 | 450 | 5600 | 22100 | 10800 |
Returning to our formula, let’s start with b first:
The top of the equation looks like this: b = 10(10800) – 220 * 450 / n(∑X2)-(∑X)2. We’ve simply filled in the values from our chart.
b = 10(10800) – 220 * 450
b = 108,000 – 99,000
b = 9,000 / n(∑X2)-( ∑X)2
Now we have to do the bottom half of the equation:
n(∑X2)-(∑X)2
=10(5600)-(220) 2
=56,000 – 48,400
=7,600
Returning to our equation:
b = 9,000 / 7,600
b = 1.1842
Now let’s move on to a:
a = 450 / 10 – 1.1842 * (220 / 10)
a = 45 – (1.1842 * 22)
a = 45 – 26.0524
a = 18.9476
So, going back to our original regression equation, Y’ = a + bX and plugging our numbers, we get:
Y’ = 18.9476 + (1.1842)X
To use this equation, we now put our desired value in for X. With an estimated 20 calls:
Y’ = 18.9476 + (1.1842)*20
Y’ = 18.9476 + 23.684
Y’ = 42.63
So, a salesperson who makes 20 calls will expect to make 42 sales.

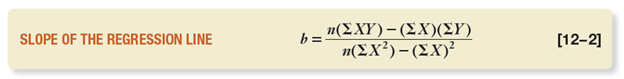
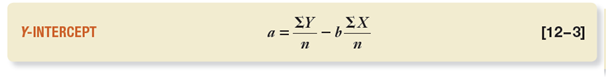
4 thoughts on “Least-Squares Regression”